AI機器學習夢幻營

# 匯入需要用到的 Python 套件
import gdown
import pandas as pd

# 從 Google Drive 下載 CSV 檔
# 用 gdown 需要提供檔案 ID，或用 --fuzzy 讓它自動判斷
url = "https://drive.google.com/file/d/12PipZYWO_I1uY83CLoMPJoEvGAOUa8cj/view?usp=drive_link"

# --fuzzy 可以讓 gdown 自動從分享連結抓到正確下載網址
gdown.download(url, "lecture_example.csv", fuzzy=True)

# 用 pandas 讀取剛剛下載的 CSV 檔
df = pd.read_csv("lecture_example.csv", encoding="utf-8-sig")

# 確認前 5 筆資料
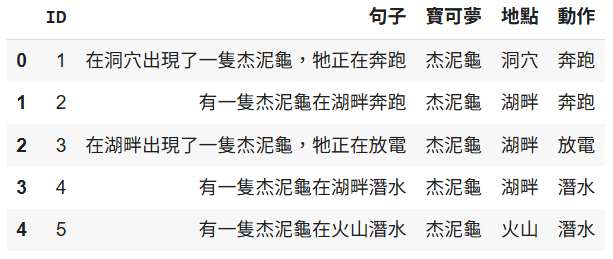
df.head()

# 定義事件 E
# 條件：句子開頭是「有一隻杰泥龜在湖畔」
E = df["句子"].astype(str).str.startswith("有一隻杰泥龜在湖畔")

# 檢查事件 E 判斷是否正確
print(E.head(10))    # 顯示前 10 筆 True/False（True 代表該筆資料符合條件）
print(E.sum())     # 計算符合條件（True）的總數

# 基本統計

total = len(df)         # 全部資料筆數 N（總共有多少句子資料）
n_E = E.sum()          # 事件 E 的筆數：True 當 1、False 當 0，相加就是符合條件的總數
p_E = n_E / total       # Evidence：P(E) = n(E) / N，事件 E 出現的比例

# 輸出檢查
print("total =", total)     # 總句子數 N
print("n_E =", n_E)       # 符合事件 E 的數量（句首「有一隻」、寶可夢=杰泥龜、地點=湖畔）
print("p_E =", p_E)       # 事件 E 的機率，應該等於 n_E / total

# 逐「動作」計算 prior, likelihood, posterior（Bayes 更新）
# 要計算的三個動作清單（或改成 df["動作"].unique().tolist()）
actions = ["奔跑", "潛水", "訓練"]

# 先建立一個空清單，之後把每個動作的結果裝進來
rows_actions = []

for act in actions:
    print(act)

# === 程式碼 五：逐一「動作」計算 Prior / Likelihood / Posteri
for act in actions:
    n_A = (df["動作"] == act).sum()# n(A)：該動作在整份資料中出現的次數

    # Prior：P(A) = n(A) / N
    # 在不知道任何條件時，這個動作出現的比例
    p_prior = n_A / total if total > 0 else float("nan")

    # n(A ∧ E)：同時滿足「動作=act 且事件 E 為 True」的筆數
    n_joint = ((df["動作"] == act) & E).sum()

    # Likelihood：P(E | A) = n(A ∧ E) / n(A)
    # 在已知「動作=act」的條件下，事件 E 發生的機率
    p_likelihood = n_joint / n_A if n_A > 0 else float("nan")

    # Posterior：P(A | E) = P(E|A) * P(A) / P(E)
    # 在已知事件 E 發生後，這個動作的後驗機率
    p_posterior = (p_likelihood * p_prior) / p_E if p_E > 0 else float("nan")


    print(f"\n正在計算： {act}")
    print("n_A =", n_A)              # 全部資料中，這個動作的數量
    print("n_joint =", n_joint)          # 同時滿足事件 E 的這個動作數
    print(f"p_prior = {p_prior:.2f}")       # 先驗機率
    print(f"p_likelihood = {p_likelihood:.2f}")  # 似然
    print(f"p_posterior = {p_posterior:.2f}")   # 後驗機率