資料專區
貝氏機器學習-上午
程式碼 一、
#下載 gdown 套件
!pip install gdown
# 匯入需要用到的 Python 套件
import gdown
import pandas as pd
# 從 Google Drive 下載 CSV 檔
# 用 gdown 需要提供檔案 ID,或用 --fuzzy 讓它自動判斷
url = "https://drive.google.com/file/d/1n60X99FfZ12DIVpdwVrmmMjTUpyzO3Qq/view?usp=sharing"
filename = "pokemon_Bug.csv" #把檔名存成一個變數
# --fuzzy 可以讓 gdown 自動從分享連結抓到正確下載網址
gdown.download(url, filename , fuzzy=True)
# 用 pandas 讀取剛剛下載的 CSV 檔
df = pd.read_csv(filename, encoding="utf-8-sig")
# 確認前 30 筆資料
df.head(30)
結果顯示

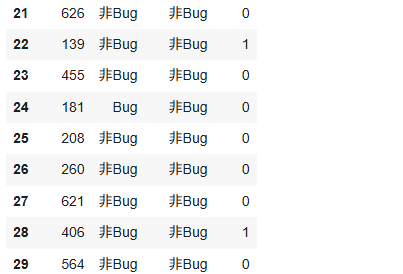
程式碼 二、
# 2) 分開蟲系 / 非蟲系
bug_df = df[df["屬性"] == "Bug"]
nonbug_df = df[df["屬性"] != "Bug"]
# 印出分組後的資料
print("=== 蟲系資料集 (bug_df) ===")
print(bug_df.head()) # 只顯示前5筆,避免太長
print("\n=== 非蟲系資料集 (nonbug_df) ===")
print(nonbug_df.head()) # 只顯示前5筆
結果顯示
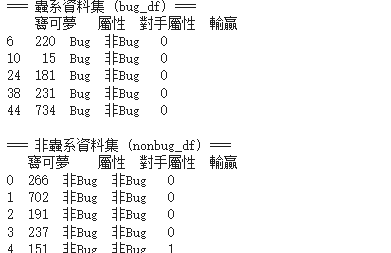
程式碼 三、
# 3) 算勝率
p_win_given_bug = (bug_df["輸贏"] == 1).mean() # 蟲系勝率
p_win_given_nonbug = (nonbug_df["輸贏"] == 1).mean() # 非蟲系勝率
print(f"P(勝利|蟲系) = {p_win_given_bug*100:.2f}%")
print(f"P(勝利|非蟲系) = {p_win_given_nonbug*100:.2f}%")
結果顯示

程式碼 四、
# 4) 固定先驗 (每種屬性等機率 1/18)
p_bug = 1/18
程式碼 五、
# 5) 貝氏翻轉公式
p_bug_given_win = p_bug * p_win_given_bug / (p_bug * p_win_given_bug + (1 - p_bug) * p_win_given_nonbug)
程式碼 六、
# 6) 輸出結果
print("=== 貝氏翻轉:P(蟲系 | 勝利) ===")
print(f"固定 P(蟲系) = {p_bug*100:.2f}%")
print(f"P(勝利|蟲系) = {p_win_given_bug*100:.2f}%")
print(f"P(勝利|非蟲系) = {p_win_given_nonbug*100:.2f}%")
print(f"P(蟲系|勝利) = {p_bug_given_win*100:.2f}%")
結果顯示

貝氏機器學習-下午
程式碼 一、
"""
Step 1:沒有孩子資料時,根據「父親目前未發病」的資訊做第一次貝氏更新
目標:Posterior = P(爸爸是Dd | 爸爸未發病)
"""
# 定義一個函數,名稱為:bayes_prior_no_kids
def bayes_prior_no_kids(p):
prior = 0.5 # Prior : P(爸爸是Dd) 初始假設
like_Dd = 1 - p # Likelihood : P(爸爸未發病 | 爸爸是Dd)
like_dd = 1.0 # Likelihood : P(爸爸未發病 | 爸爸是dd)
# Evidence :
# P(爸爸未發病) = P(爸爸是Dd)*P(爸爸未發病|爸爸是Dd) + (1-P(爸爸是Dd))*P(爸爸未發病|爸爸是dd)
evidence = prior * like_Dd + (1 - prior) * like_dd
# Posterior :
# P(爸爸是Dd | 爸爸未發病) = [P(爸爸是Dd) × P(爸爸未發病|爸爸是Dd)] / P(爸爸未發病)
posterior = (prior * like_Dd) / evidence
return posterior
程式碼 二、
"""
Step 2:計算小新發病機率
目標:Posterior = P(小新發病|爸爸未發病)
"""
# 定義一個函數,名稱為:calc_initial_risk
def calc_initial_risk(p):
# 這是上一步得到的 Posterior [P(爸爸是Dd|爸爸未發病)],作為此步的Prior
prob_father_Dd = bayes_prior_no_kids(p)
# P(小新遺傳到D|爸爸是Dd)
prob_inherit_D = 0.5
# P(小新發病機率)
# p為疾病穿透力=P(小新發病|小新是Dd)
risk = prob_father_Dd * prob_inherit_D * p
# 函數回傳兩個數值
return prob_father_Dd, risk
程式碼 三、
# =========================================
# Step 3:觀察到「已有 n 個健康小孩」後,再做一次貝氏更新
# 目標:Posterior = P(爸爸是Dd|n個健康小孩)
# Step 4:用更新機率計算下一個小孩得病機率
# 目標:Risk = P(下一個小孩發病)
# =========================================
# 定義一個函數,名稱為:calc_updated_risk
def calc_updated_risk(p, n):
# Step 3
prior = 0.5 # Prior:P(爸爸為Dd)
like_Dd =(1-p)* (1 - p/2) ** n # Likelihood:P(有n個小孩健康,爸爸健康|爸爸為Dd)
like_dd = 1.0 # Likelihood:P(有n個小孩健康,爸爸健康|爸爸為dd)
# Evidence:P(有n個小孩健康)
evidence = prior * like_Dd + (1 - prior) * like_dd
# Posterior:P(爸爸為Dd|有n個小孩健康)
posterior = (prior * like_Dd) / evidence
# Step 4
# 下一胎得病機率 = Posterior × P(下一個小孩遺傳到D|爸爸是Dd) × P(下一個小孩發病|下一個小孩是Dd)
risk = posterior * 0.5 * p
return posterior, risk
程式碼 四、
# 輸出結果
# 顯示整體風險分析結果(Bayes 概率計算後的輸出)
# p : 疾病的穿透力(penetrance),0~1 之間 ; n : 已知健康的小孩數量
def show_results(p, n):
print(f"參數:穿透力 p = {p}, 健康小孩數 n = {n}\n")
# A. 初始(僅用「爸爸未發病」作為證據)
prob_father_Dd_init, risk_init = calc_initial_risk(p)
# B. 更新(再加入「n 個孩子皆健康」作為新證據)
prob_father_Dd_updated, risk_updated = calc_updated_risk(p, n)
# --- 列印初始結果 ---
print("► 計算小新發病機率:")
print(f" - Posterior P(父親是Dd | 未發病) = {prob_father_Dd_init*100:.2f}%")
print(f" - P(小新得病) = {risk_init*100:.2f}%")
# --- 列印更新後結果 ---
print(f"\n► 已有 {n} 個健康小孩(加入新證據):")
print(f" - Posterior P(父親是Dd | n 健康) = {prob_father_Dd_updated*100:.2f}%")
print(f" - P(第{n+1}小孩得病) = {risk_updated*100:.2f}%")
程式碼 五、
# === 參數設定 ===
p = 0.6 # 穿透力(0~1)
n = 3 # 已健康小孩數
# === 執行計算 ===
show_results(p, n)
結果顯示







